|
|
|
Let ![]() and
and ![]() be Polynomials of Degrees
be Polynomials of Degrees ![]() and
and ![]() with
Coefficients
with
Coefficients ![]() , ...,
, ..., ![]() and
and ![]() , ...,
, ..., ![]() . Take the contour in the upper half-plane, replace
. Take the contour in the upper half-plane, replace ![]() by
by ![]() ,
and write
,
and write
![]() . Then
. Then
| (1) |
|
|
|
|
|
|
|
|
(2) |
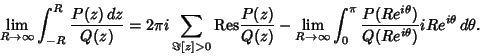
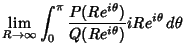 |
|||
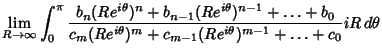 |
|||
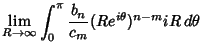 |
|||
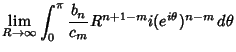 |
(3) |
and set
| (4) |
| (5) |
| (6) |
![\begin{displaymath}
\int_{-\infty}^\infty {P(z)\,dz\over Q(z)} = 2\pi i\sum_{\Im[z]> 0} {\rm Res} \left[{P(z)\over Q(z)}\right]
\end{displaymath}](c2_1634.gif) |
(7) |
| (8) |
![\begin{displaymath}
\int_{-\infty}^\infty {P(z)\over Q(z)} e^{iaz}\,dz
= 2\pi i...
...[z]> 0}\mathop{\rm Res}\left[{{P(z)\over Q(z)} e^{iaz}}\right]
\end{displaymath}](c2_1638.gif) |
(9) |
Since this must hold separately for Real and Imaginary Parts, this result can be
extended to
![\begin{displaymath}
\int_{-\infty}^\infty {P(x)\over Q(x)} \cos(ax)\,dx = 2\pi\R...
...! {\rm Res}
\left[{{P(z)\over Q(z)} e^{iaz}}\right]}\right\}
\end{displaymath}](c2_1639.gif) |
(10) |
![\begin{displaymath}
\int_{-\infty}^\infty {P(x)\over Q(x)} \sin(ax)\,dx = 2\pi\I...
... {\rm Res}
\left[{{P(z)\over Q(z)} e^{iaz}}\right]}\right\}.
\end{displaymath}](c2_1640.gif) |
(11) |
| (12) |
See also Cauchy Integral Formula, Cauchy Integral Theorem, Inside-Outside Theorem, Jordan's Lemma, Residue (Complex Analysis), Sine Integral
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill,
pp. 353-356, 1953.
|
|
|
© 1996-9 Eric W. Weisstein