Yff Points

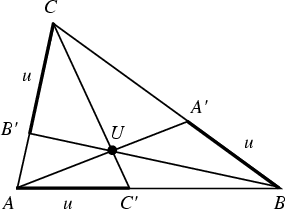
Let points $A'$, $B'$, and $C'$ be marked off some fixed distance $x$ along each of the sides $BC$, $CA$, and $AB$. Then the lines $AA'$, $BB'$, and $CC'$ concur in a point $U$ known as the first Yff point if

$$x^3=(a-x)(b-x)(c-x).$$ (1)

This equation has a single real root $u$, which can by obtained by solving the Cubic Equation

$$f(x)=2x^3-px^2+qx-r=0,$$ (2)

where

$$p = a+b+c$$ (3)

$$q = ab+ac+bc$$ (4)

$$r = abc.$$ (5)

The Isotomic Conjugate Point $U'$ is called the second Yff point. The Triangle Center Functions of the first and second points are given by

$$\alpha={1\over a}\left({c-u\over b-u}\right)^{1/3}$$ (6)

and

$$\alpha'={1\over a}\left({b-u\over c-u}\right)^{1/3},$$ (7)

respectively. Analogous to the inequality $\omega\leq\pi/6$ for the Brocard Angle $\omega$, $u\leq p/6$ holds for the Yff points, with equality in the case of an Equilateral Triangle. Analogous to

$$\omega<\alpha_i<\pi-3\omega$$ (8)

for $i=1$, 2, 3, the Yff points satisfy

$$u<a_i<p-3u.$$ (9)

Yff (1963) gives a number of other interesting properties. The line $UU'$ is Perpendicular to the line containing the Incenter $I$ and Circumcenter $O$, and its length is given by

$$\overline{UU'}={4u\overline{IO}\Delta\over u^3+abc},$$ (10)

where $\Delta$ is the Area of the Triangle.

See also Brocard Points, Yff Triangles

References

Yff, P. ``An Analog of the Brocard Points.'' Amer. Math. Monthly 70, 495-501, 1963.