If 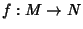 , then the tangent map
, then the tangent map 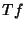 associated to
associated to 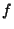 is a Vector Bundle Homeomorphism
is a Vector Bundle Homeomorphism 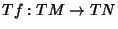 (i.e., a Map between the Tangent Bundles of
(i.e., a Map between the Tangent Bundles of 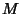 and
and 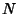 respectively). The
tangent map corresponds to Differentiation by the formula
respectively). The
tangent map corresponds to Differentiation by the formula
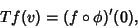 |
(1) |
where 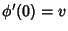 (i.e.,
(i.e., 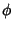 is a curve passing through the base point to
is a curve passing through the base point to 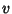 in
in 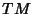 at time 0 with velocity
at time 0 with velocity 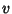 ).
In this case, if
).
In this case, if 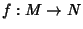 and
and 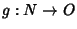 , then the Chain Rule is expressed as
, then the Chain Rule is expressed as
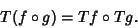 |
(2) |
In other words, with this way of formalizing differentiation, the Chain Rule can be remembered by saying that
``the process of taking the tangent map of a map is functorial.'' To a topologist, the form
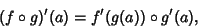 |
(3) |
for all 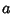 , is more intuitive than the usual form of the Chain Rule.
, is more intuitive than the usual form of the Chain Rule.
See also Diffeomorphism
References
Gray, A. ``Tangent Maps.'' §9.3 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 168-171, 1993.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , then the tangent map
, then the tangent map ![]() associated to
associated to ![]() is a Vector Bundle Homeomorphism
is a Vector Bundle Homeomorphism ![]() (i.e., a Map between the Tangent Bundles of
(i.e., a Map between the Tangent Bundles of ![]() and
and ![]() respectively). The
tangent map corresponds to Differentiation by the formula
respectively). The
tangent map corresponds to Differentiation by the formula