Polygonal Spiral

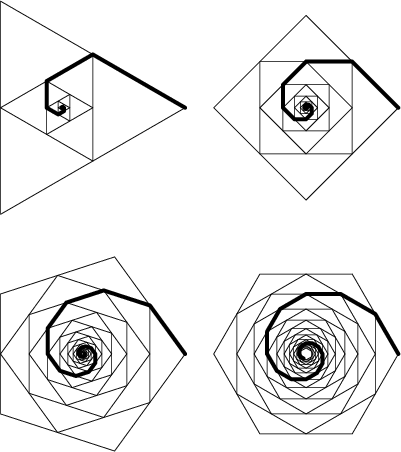
The length of the polygonal spiral is found by noting that the ratio of Inradius to Circumradius of a regular Polygon of $n$ sides is

$${r\over R}={\cot\left({\pi\over n}\right)\over\csc\left({\pi\over n}\right)} = \cos\left({\pi\over n}\right).$$ (1)

The total length of the spiral for an $n$-gon with side length $s$ is therefore

$$L={\textstyle{1\over 2}}s\sum_{k=0}^\infty \cos^k\left({\pi\... ...ght)={s\over 2\left[{1-\cos\left({\pi\over n}\right)}\right]}.$$ (2)

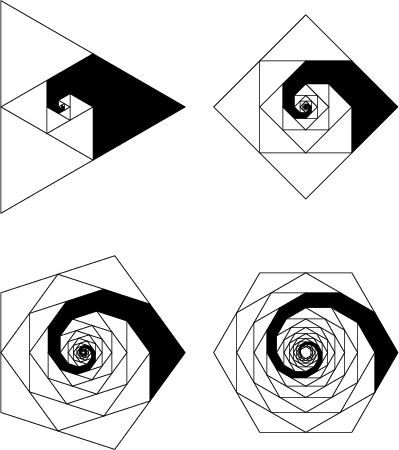
Consider the solid region obtained by filling in subsequent triangles which the spiral encloses. The Area of this region, illustrated above for $n$-gons of side length $s$, is

$$A={\textstyle{1\over 4}}s^2\cot\left({\pi\over n}\right).$$ (3)

References

Sandefur, J. T. ``Using Self-Similarity to Find Length, Area, and Dimension.'' Amer. Math. Monthly 103, 107-120, 1996.