§ 2   Field Theory Preliminary

 

1. Basic Concepts of Field Theory and Gradient, Divergence and Curl

 

[ scalar field ]   Each point M ( x , y , z ) in the space area D corresponds to a quantity value ( x , y , z ) , which constitutes a scalar field on this space area D , using the point M ( x,y , z ) is represented by the scalar function ( x , y , z ) . If the position of M is determined by the vector radius r , the scalar can be regarded as a function of the variable vector r = ( r ).

For example, the temperature field u ( x , y , z ), the density field , and the electric potential field e ( x , y , z ) are all scalar fields .

    [ Vector field ]   Each point M ( x , y , z ) in space area D corresponds to a vector value r ( x , y , z ) , which constitutes a vector field on this space area D , using point M ( x , y , z ) of the vector function r ( x , y , z ) is represented . If the position of M is determined by the vector radius r , the vector r can be regarded as the vector function r ( r of the variable vector r )) :

r ( r )= X ( x , y , z ) i + Y ( x , y , z ) j + Z ( x , y , z ) k

    For example, the velocity field ( x , y , z ) , the electric field E ( x , y , z ) , the magnetic field H ( x , y , z ) are all vector fields .

As in the case of scalar fields, the concept of a vector field is essentially the same as that of a vector function . These terms ( scalar field, vector field ) are used to preserve their own origin and physical meaning .

[ gradient ]

grad = ( , , ) = = i + j + k

In the formula = i + j + k is called the Hamiltonian operator , also known as the Nepra operator. Grad is denoted as del in some books and periodicals .

    The direction of grad coincides with the normal direction N of the isometric plane = C passing through the points ( x , y , z ) , and points to the increasing side, which is the direction with the greatest rate of change of the function, and its length is equal to .

Gradients have properties:

grad( + ) = grad + grad ( , is a constant )   

             grad( ) = grad + grad

             grad F ( ) =

[ Directional Derivative ]

= l · grad = cos + cos + cos

where l = (cos , cos , cos ) is the unit vector of direction l , , , which is the direction angle .

The directional derivative is the law of change in the direction l , which is equal to the projection of the gradient in the direction l .

[ divergence ]

div r = + + = r = div ( X , Y , Z )

where is the Hamiltonian .

    Divergence has the property:

    div( a + b ) = div a + div b ( , is a constant )   

    div( a ) = div a + a grad

    div ( a × b ) = b rot a − a rot b _

[ curl ]

       rot r = ( ) i + ( ) j + ( ) k = × r =

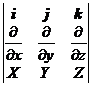
where is Hamiltonian operator, curl is also called vorticity, rot r is denoted as curl r in some books and periodicals .

Curl has the properties:

rot( a + b ) = rot a + rot b ( , is a constant )   

rot( a ) = rot a + a × grad

rot( a × b ) = ( b · ) a − ( a · ) b + (div b ) a − (div a ) b

[ Gradient, divergence, curl mixed operation ] The   operation grad acts on a scalar field to generate a vector field grad , the operation div acts on a vector field r to generate a scalar field div r , and the operation rot acts on a vector field r to generate a new vector field

rot r . The mixed operation formula of these three operations is as follows:

div rot r = 0

rot grad = 0

div grad = + + =

grad div r = ( r )

rot rot r = × ( × r )

div grad( + ) = div grad + div grad (     , is a constant )

div grad( )= div grad + div grad +2 grad · grad

grad div r - rot rot r = r

where is the Hamiltonian, and = = 2 ^is the Laplace operator . 

    [ Potential field ( conservation field )]   If the vector field r ( x , y , z ) is the gradient of a scalar function ( x , y , z ) , that is

r =grad or X =, Y =, Z =

Then r is called the potential field, and the scalar function is called the potential function of r .

The necessary and sufficient conditions for the vector field r to be a potential field are: rot r = 0, or

 = , = , =

Potential function calculation formula

( x , y , z ) = ( x ₀ , y ₀ , z ₀ ) + +

+

[ No scatter ( tubular field )] If   the divergence of the vector field r is zero, that is, div r = 0 , then r is called a scatter-free field . At this time, there must be a scatter-free field T , so that r = rot T , for any point M has

T =

where r is the distance from dV to M , and the integration is performed over the entire space .

     [ Irrotational field ]   If the curl of the vector field r is zero, that is, rot r = 0 , then r is called an irrotational field . The potential field is always an irrotational field, and there must be a scalar function , so that r = grad , and for any point M we have

=-

where r is the distance from d V to M , and the integration is performed over the entire space .

 

2. Expressions of gradient, divergence and curl in different coordinate systems

 

    1 . unit vector transformation

    [ General formula ]   Assume that x = f ( ), y = g ( ), z = h ( ) to continuously map a region of ( ) space to a region D of ( x , y , z ) space , and Assuming that f , g , h have continuous partial derivatives, because the correspondence is one-to-one, we have   

= ( x , y , z ) ,

Assuming that there are also continuous partial derivatives, then we have

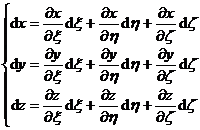
or inverse transform

 

The unit vectors along the d x , dy , d z directions are denoted as i , j , k , and the unit vectors along the directions are denoted as

    [ Unit vector of cylindrical coordinate system ]   For cylindrical coordinate system ( Fig. 8.11)

   

The unit vector is

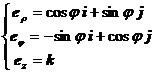
    Their partial derivatives are

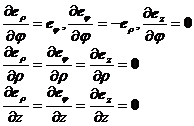
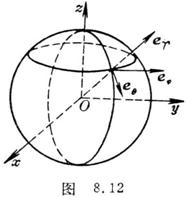
    [ Unit vector of spherical coordinate system ]   For spherical coordinate system ( Fig. 8.12)

         

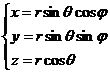
The unit vector is

        

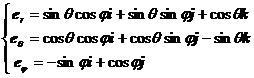
Their partial derivatives are

        

    2 . Coordinate transformation of vectors

[ General formula ] A   vector expressed by the ( x , y , z ) coordinate system can be expressed by the ( ) coordinate system :

= ( , _y , _z ) = i + _y j + _z k =

in the formula

[ Exchange of Cylindrical Coordinate System and Cartesian Coordinate System ]   Transformation Formula from Cylindrical Coordinate System to Cartesian Coordinate System

Transformation formula from Cartesian coordinate system to cylindrical coordinate system

[ Exchange of spherical coordinate system and rectangular coordinate system ] Transformation formula from spherical coordinate system to rectangular coordinate system

Transformation formula from rectangular coordinate system to spherical coordinate system

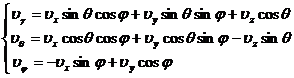
3 . Expressions of various operators in different coordinate systems

Let U = U ( x , y , z ) be a scalar function and V = V ( x , y , z ) be a vector function .

[ Expressions of various operators in the cylindrical coordinate system ]

Hamiltonian = + + 

Gradient grad U = U = + +       

Divergence div V = · V = _       

Curl rot V = × V = + + _       

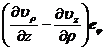
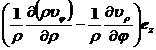
Laplacian U = div grad U = 

[ Expressions of various operators in spherical coordinates ]

Hamiltonian = + + 

Gradient grad U = U = + +       

Divergence div V = · V =       

Curl rot V = × V = _       

+

+

Laplacian U = div grad U 

 =

 

3. Curve integral, surface integral and volume derivative

 

[ Curve integral of a vector and its calculation formula ] The curvilinear integral of a   vector field r ( r ) along a curve is defined as

r ( r )·d r = r ()· r _{i -1}

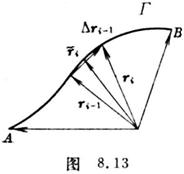where ri _-1 = ri - _{ri -1} , the right limit _{is independent} of the choice of the curve

From A to B ( Fig. 8.13)

If the vector function R ( r ) is continuous ( that is, its three components are

continuous function ), the curve is also continuous and has continuous rotation

tangent , the curve integral

exist .

If R ( r ) is a force field, then P = equals to

The work done by a force R when a particle moves along G.

    The formula for calculating the vector curve integral is as follows:

        =

        = + ( Figure 8.14) 

        = -

        = +

        = k ( k    is a constant )

[ Circulation of the vector ]  If G is a closed curve, then the curve integral along the curve G

=

It is called the circulation of the vector field R ( r ) along the closed curve G.

    The circulation of the potential field along any closed curve is equal to zero . If R ( r ) is a potential field and its potential function is , then the curve integral

             = = ( B ) - ( A )

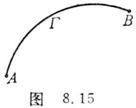
It has nothing to do with the path connecting points A and B , but only depends on the path between points A and B.

position ( Figure 8.15).

    [ Surface integral of a vector ]   Let S be a surface, let N = denote the normal unit vector of a point on the surface S , V and d S = N d S denote the area vector element . Let ( r ) = ( x , y , z ) is a continuous scalar function defined on the surface S , R ( r )=( X ( x , y , z ), Y ( x , y , z ), Z( x , y , z )) is a continuous vector function defined on the surface S , the surface integral has the following three forms:

    1 Flux ( or flow ) of a scalar field 

        d S = d y d zi + d z d x j + d x d y k _

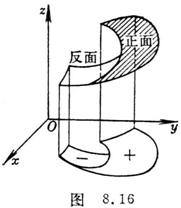
where S _yz , S _zx , S _xy represent the surface S in the Oyz plane, Ozx plane, respectively ,

Projection on the Oxy plane . The sign of S _xy is specified as follows: when looking from the positive z axis

When looking to the side, what you see is the front of the surface S , consider S _xy to be positive, if

If you see the opposite side of the surface, consider S _xy to be negative ( Figure 8.16).

    2   Scalar Flux of a Vector Field

    R d S = X d y d z + Y d z d x + Z d x d y _

The meanings of S _yz etc. in the formula are the same as 1 .

3   Vector flux of a vector field

R ×d S =( Z j - Y k )d y d z +( X k - Z i )d z d x +( Y i - X j )d x d y

The meanings of S _yz etc. in the formula are the same as 1 .

    [ Volume Derivative of Vector ]   If S is a closed surface enclosing volume V and contains point r , then the ratio of the surface integral ( d S , R d S , R × d S ) along the closed surface S to the volume V , when The limit when V tends to zero ( i.e. its diameter 0 ) is called the volume derivative ( or spatial derivative ) of the scalar field ( or vector field R ) at point r ).

    1 The volume derivative of a scalar field is its gradient: 

grad =

    2 One of the volume derivatives of a   vector field R is its divergence:

div R =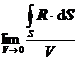

    3 Another volume derivative of the   vector field R is its curl:

rot R = -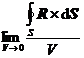

 

4. Integral Theorem of Vectors

 

    [ Gaussian formula ]

R d V = R · d S = R · N d S

which is

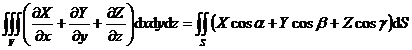
where S is the boundary surface of the space region V , and N = is

normal unit vector at a point on S , R ( r )=( X ( x , y , z ), Y ( x , y , z ), Z ( x , y , z ))

There are continuous partial derivatives on V + S.

    [ Stokes formula ]

rot R · d S = rot R · N d S = R · d r

which is

   

  =

  =

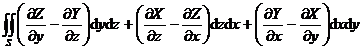
In the formula, S is one side of a certain surface, L is the closed boundary curve of the surface S ( the positive direction of L and N form a right-handed system ). Each point of S has a tangent surface, and its direction continuously depends on the points on the surface, and the boundary Each point on the curve L has a tangent ( Fig. 8.17). R ( r )=( X ( x , y , z ), Y ( x , y , z ), Z ( x , y , z )) at the surface of the All points are single-valued and have continuous partial derivatives at points close enough to S.

    [ Green formula ]

        · dS = _

        · dS = _

In the formula, S is the boundary surface of the space region V , which is two scalar functions. It has continuous partial derivatives on S and second-order continuous partial derivatives on V. It is the Laplace operator, especially

· dS = _

which is