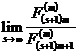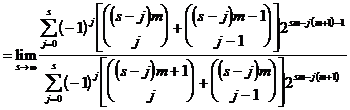§2 Continued Fractions
[ Simple Continued Fraction ] If a is a real number ( rational or irrational ), it can be expressed as a simple continued fraction
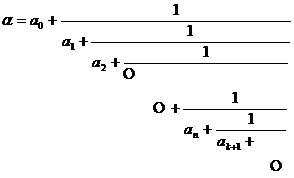
abbreviated as ![]()
or
![]()
where is an integer , which is a positive integer .![]()
![]()
If a is a rational number , it must be developable into a finite continuous fraction![]()
![]()
where is a series of incomplete quotients obtained by a series of equations (1) obtained by rolling and dividing . If the last incomplete quotient is specified to be greater than 1, that is, at that time , it can be written as![]()
![]()
![]()
The table method is unique .
If a is an irrational number , it can be developed into an infinitely continuous fraction , and the representation is unique .
[ Complete quotient and incomplete quotient ] The ith incomplete quotient of a is called in the simple continued fraction (2) . The number is called the nth complete quotient of a . Obviously .![]()
![]()
![]()
The relationship between perfect quotient and incomplete quotient :

![]() ( n =0,1,2,…)
( n =0,1,2,…)
where is the numerator and denominator of the nth asymptotic fraction of a ( see below ) .![]()
[ Asymptotic Fraction and Best Asymptotic Fraction ] Intercept in Simple Continued Fraction (1)
![]()
Call it the nth asymptotic fraction of a . Asymptotic fractions are all reduced fractions .
1. Equations and inequalities for asymptotic fractions of °
![]()

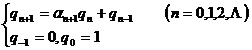

( at the time )![]()
![]() ( when a is a real quadratic irrational number )
( when a is a real quadratic irrational number )


( In the formula, it is a decreasing function of n . When a is a rational number , this formula is only valid at that time , )![]()
![]()
![]()
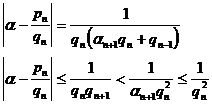
2 ° set and then ![]()
![]()
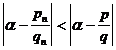
So among all the fractions whose denominator is not greater than a , the closest to a ( called the best asymptotic fraction ).![]()
![]()
![]()
One of the two adjacent asymptotic fractions of 3 ° a must be suitable for ![]()
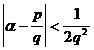
One of the three adjacent asymptotic fractions of 4 ° a must be suitable for ![]()

5 ° Let a be a real number , a rational number , and M be a positive integer . If a is suitable for the inequality ![]()
![]()
Then at least one of the incomplete quotients of a developed into a continuous fraction is greater than M - 2 .
[ Periodic continuous fraction and its necessary and sufficient conditions ] At that time , if , then the continuous fraction![]()
![]()
![]()
is called the periodic continuous fraction with period k , denoted as
![]() (3)
(3)
When l=0 , equation (3) is called pure periodic continued fraction , and when l =1 , equation (3) is called quasi-pure periodic continued fraction .
The necessary and sufficient conditions for a 1 ° real number a to be developable into periodic continuous fractions are : a is a root of a quadratic irreducible polynomial over the field of rational numbers .
The necessary and sufficient conditions for a 2 ° real quadratic irrational number a to be developed into a pure periodic continuous fraction are : a > 1 and , where a ' is a real conjugate of a . ![]()
The necessary and sufficient conditions for a 3 ° real quadratic irrational number a to be developed into a quasi-pure periodic continuous fraction are : a '<[ a ]-1, where a ' is the conjugate real number of a , and [ a ] is the integer part of a .
[ , ![]() Continued fraction of e and p ]
Continued fraction of e and p ]
1 ° is set as a , then ![]()
![]()
2 ° Let e be the base of the natural logarithm , then
![]()
The general formula for the incomplete quotient is
![]()
3 ° Let p be the pi , then
![]()
Its asymptotic fraction is
![]()
[ Continued fraction table of integral bases of quadratic field Q( )![]() ]
]
|
w |
Continued Fraction Representation |
w |
Continued Fraction Representation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[4,7] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ The Golden Ratio and the Fibonacci Sequence ]
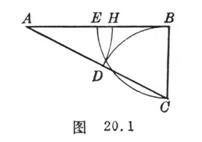
1 ° The division of the line segment AB into the ratio between the inside and outside ( ie ) is called the golden section . That is to solve the algebraic equation
![]()
|
|
![]()
a root of
![]()
The geometric drawing of the golden section is shown in Figure 20.1 ( E is the midpoint of AB ).
2 ° by the recurrence relation
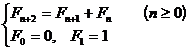
the resulting sequence
![]()
is called a Fibonacci sequence . Its general term is expressed as
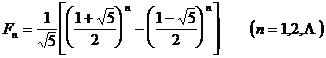
3 ° At that time , . ![]()
![]()
4 ° is the best asymptotic fraction of , and is the best asymptotic fraction of . ![]()
![]()
![]()
![]()
5 ° Let a, b be natural numbers , by the recurrence relation
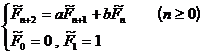
The general term expression for the resulting sequence is
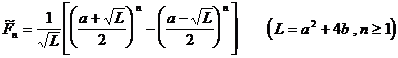
And it has properties : at that time , .![]()
![]()
[ Generalized Fibonacci sequence ] by the recurrence relation

The resulting sequence is called the m -level generalized Fibonacci sequence . Its general term is expressed as
Let w be the equation
![]()
the only positive real root of , then
w =