§ 3    Arc method and average method of curve fitting

 

1. The arc method of curve fitting

 

Circular fitting is a geometric method that depicts a fitted curve through observation points ( model points ) . It replaces curves with segmented arcs and makes two adjacent arcs have a common tangent. This approach boils down to the following three situations :

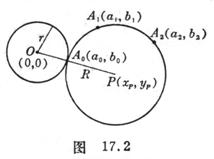
   Given circle O and two points outside the circle , , find the circle P , make it pass through the points , and be tangent ( circumscribed or inscribed ) with circle O ( Fig. 17.2 ) .

 Let the radius of the circle O be r and the coordinates of the point O to be ( 0,0 ) . remember

                             

       

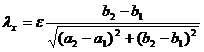
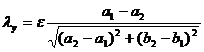
, the symbol is inscribed or excised. remember again

           

in the formula

           

           

           

then

( i ) The coordinates of the center of the circle P are

                

( ii ) The radius R of the circle P is

        

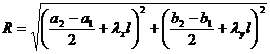
( iii ) The coordinates of the tangent point are

         

in 

            

            

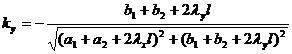
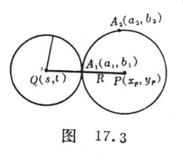
  Knowing the circle Q and a point outside the circle , find the circle P so that it passes through the fixed point and is tangent to the circle Q at the fixed point ( Figure 17.3 ) .

   Let the coordinates of the center of the circle Q be ( s, t ) , then

( i ) The coordinates of the center of the circle P are

  

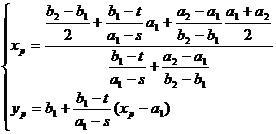
                                                                          ( ii ) The radius R of the circle P is

          

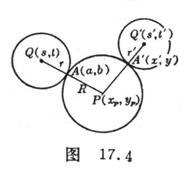
   Knowing the circle Q and the circle , find the circle P so that it is tangent to the circle and to the circle Q at a fixed point ( Fig. 17.4 ) .

 Let the coordinates of the center of the circle Q be ( s, t ) and the radius be r ; the coordinates of the center of the circle are and the radius is . remember again

      

         

         

         

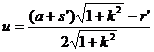
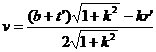
then

( i ) The coordinates of the center of the circle P are

            

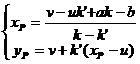
( ii ) The radius R of the circle is

            

( iii ) The coordinates ( x', y' ) of the tangent point A' are

            

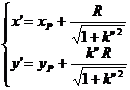
in the formula            

 

Second, the average method of curve fitting

 

   [ Linear ] If a series of data for two variables ( x, y ) are known to be

 

x	…
y	…

Suppose x, y satisfy a linear relationship

                                

Then a and b are determined by the following equations :

             

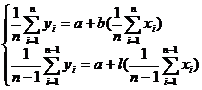
   The dispersion of the ordinate between the straight line obtained by this method and each point

                                

The algebraic sum is zero.

[ Parabolic ]   If the straight line does not fit the trend of the known data, then the optional polynomial  

                                

to fit. For example, take the empirical curve as a quadratic polynomial

                            

a,b,c can be determined by the following three-dimensional linear equations :